Bài 2: Hai đường thẳng vuông góc - Lý thuyết Toán học 11 - Tìm đáp án,

1. Góc thân ái hai vectơ

Cho \(\vec u\) và \(\vec v\) là nhị vectơ vô không khí. Từ một điểm A bất kì vẽ \(\overrightarrow {AB} = \overrightarrow u ,\overrightarrow {AC} = \overrightarrow v\). Khi bại tao gọi góc \(\widehat {BAC}(0 \le \widehat {BAC} \le {180^0})\) là góc thân ái nhị vecto vectơ \(\vec u\) và \(\vec v\), kí hiệu là \(\left ( \vec u ;\vec v \right )\). Ta có: \(\left ( \vec u ;\vec v \right )=\widehat {BAC}\).

Bạn đang xem: Bài 2: Hai đường thẳng vuông góc - Lý thuyết Toán học 11 - Tìm đáp án,

2. Tích vô vị trí hướng của nhị vectơ

a) Định nghĩa tích vô vị trí hướng của nhị vectơ

Tích vô vị trí hướng của nhị vectơ \(\vec u\) và \(\vec v\) đều không giống vectơ-không là một số trong những được kí hiệu là \(\vec u .\vec v\) xác dịnh bởi:

\(\vec u.\vec v = \left| {\vec u} \right|.\left| {\vec v} \right|.\cos (\overrightarrow u .\vec v)\)

Nếu \(\vec u= \vec0\) hoặc \(\vec v= \vec0\) thì tao quy ước 

\(\vec u.\vec v=0.\)

b) Tính chất tích vô vị trí hướng của nhị vectơ

Với tía vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c\) trong không khí và với từng số k tao có:

• \(\overrightarrow a .\overrightarrow b = \overrightarrow b .\overrightarrow a\) (tính hóa học phú hoán).
• \(\overrightarrow a (\overrightarrow b + \overrightarrow c ) = \overrightarrow a .\overrightarrow b + \overrightarrow a .\overrightarrow c\) (tính hóa học phân phối).
• \((k.\overrightarrow a ).\overrightarrow b = k.(\overrightarrow a .\overrightarrow b ) = \overrightarrow a .k\overrightarrow b .\)
• \({\overrightarrow a ^2} \ge 0,{\overrightarrow a ^2} = 0 \Leftrightarrow \overrightarrow a = \overrightarrow 0.\)

c) Ứng dụng của tích vô hướng

Xác lăm le góc thân ái nhị vectơ \(\vec u\) và \(\vec v\) bằng \(\cos (\overrightarrow u .\vec v)\) theo đòi công thức: 

\(\cos (\overrightarrow u .\vec v) = \frac{{\vec u.\vec v}}{{\left| {\vec u} \right|\left| {\vec v} \right|}}\)   

3. Vectơ chỉ phương của lối thẳng

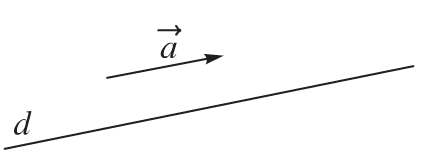
Vectơ \(\overrightarrow a \ne \overrightarrow 0\) được gọi là vectơ chỉ phương của đường thẳng liền mạch d nếu như giá chỉ của vectơ \(\overrightarrow a\) song tuy vậy hoặc trùng với đường thẳng liền mạch d.

Nếu \(\overrightarrow a\) là vectơ chỉ phương của đường thẳng liền mạch d thì vectơ \(k\overrightarrow a\) với \(k \ne 0\) cũng là 1 vectơ chỉ phương của d.

Một đường thẳng liền mạch d vô không khí trọn vẹn xác lập được nếu như biết một điểm A nằm trong d và một vectơ chỉ phương \(\overrightarrow a\) của d.

4. Góc thân ái hai tuyến đường thẳng

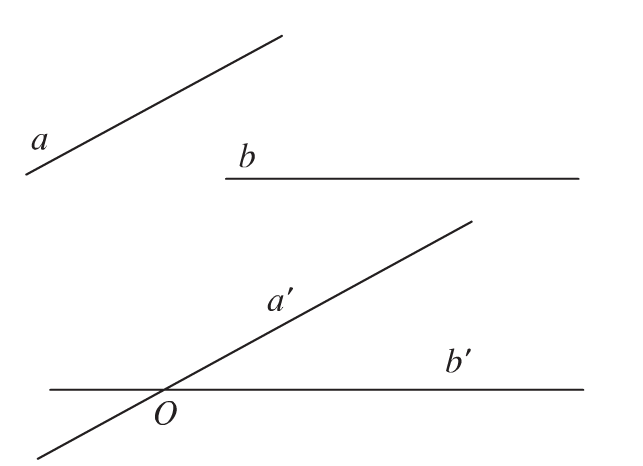
Góc thân ái hai tuyến đường trực tiếp a và b vô không khí là góc thân ái hai tuyến đường trực tiếp a’ và b’ nằm trong trải qua một điểm bất kì thứu tự tuy vậy song với a và b.

5. Hai đường thẳng liền mạch vuông góc

a) Định nghĩa

Hai đường thẳng liền mạch a và b gọi là vuông góc cùng nhau nếu như góc thân ái bọn chúng vì như thế 90⁰.

Ta kí hiệu là: \(b \bot a\) hoặc \(a \bot b.\)

b) Tính chất

• Nếu \(\vec u\) và \(\vec v\) lần lượt là những vectơ chỉ phương của hai tuyến đường trực tiếp a và b thì: \(a \bot b \Leftrightarrow \overrightarrow u .\overrightarrow v = 0.\)
• Cho hai tuyến đường trực tiếp tuy vậy tuy vậy. Nếu một đường thẳng liền mạch vuông góc với đường thẳng liền mạch này thì cũng vuông góc với đường thẳng liền mạch bại.
• Hai đường thẳng liền mạch vuông góc nhau thì rất có thể hạn chế nhau hoặc chéo cánh nhau.

6. Bài luyện minh họa

Ví dụ 1:

Cho hình lập phương ABCD.EFGH. Hãy xác lập góc trong số những cặp vectơ sau đây:

a) \(\overrightarrow {AB} ,\overrightarrow {EG} .\)

c) \(\overrightarrow {AB} ,\overrightarrow {DH}\).

Hướng dẫn giải:

a) Vì EG // AC nên góc giữa 

\(\overrightarrow {AB} ,\overrightarrow {EG}\) cũng vì như thế góc giữa 

\(\overrightarrow {AB}\) và \(\overrightarrow {AC}\)

Vậy \(\left( {\overrightarrow {AB} ;\overrightarrow {EG} } \right) = \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = {45^0}.\)

b)  Vì AB // DG nên góc giữa \(\overrightarrow {AB} ,\overrightarrow {DH}\) cũng vì như thế góc giữa \(\overrightarrow {DC}\) và \(\overrightarrow {DH}\)

Vậy \(\left( {\overrightarrow {AB} ;\overrightarrow {DH} } \right) = \left( {\overrightarrow {AB} ;\overrightarrow {DH} } \right) = {45^0}.\)

Ví dụ 2:

Cho hình chóp tam giác S.ABC đem SA = SB = SC và đem \(\widehat {{\rm{ASB}}} = \widehat {BSC} = \widehat {CSA}.\)

Chứng minh rằng: \(SA \bot BC, SB\bot AC, SC \bot AB.\)

Hướng dẫn giải:

Xét những tích vô hướng: 

\(\overrightarrow {SA} .\overrightarrow {BC} ,\overrightarrow {SB} .\overrightarrow {AC} ,\overrightarrow {SC} .\overrightarrow {AB} .\)

Ta có: 

\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {SA} .\overrightarrow {BC}  = \overrightarrow {SA} .(\overrightarrow {SC}  - \overrightarrow {SB} )\\
 = \overrightarrow {SA} .\overrightarrow {SC}  - \overrightarrow {SA} .\overrightarrow {SB} 
\end{array}\\
\begin{array}{l}
 = \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {SC} } \right|.\cos \widehat {CSA}\\
\,\,\,\,\,\,\,\,\, - \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {SB} } \right|\cos \widehat {ASB}
\end{array}
\end{array}\)

Theo giá chỉ thuyết: \(\left| {\overrightarrow {SB} } \right| = \left| {\overrightarrow {SC} } \right|\)

Và: \(\cos \widehat {CSA} = \cos \widehat {ASB} \Rightarrow \overrightarrow {SA} .\overrightarrow {BC}  = 0\)

Vậy: \(SA \bot BC.\)

Chứng minh tương tự động tao có: 

\(SB\bot AC, SC \bot AB.\)

Ví dụ 3:

Cho tứ diện ABCD đem AB ⊥ AC và AB ⊥ BD. Gọi P.. và Q thứu tự là trung điểm của AB và CD. Chứng minh rằng AB và PQ là hai tuyến đường trực tiếp vuông góc cùng nhau.

Hướng dẫn giải:

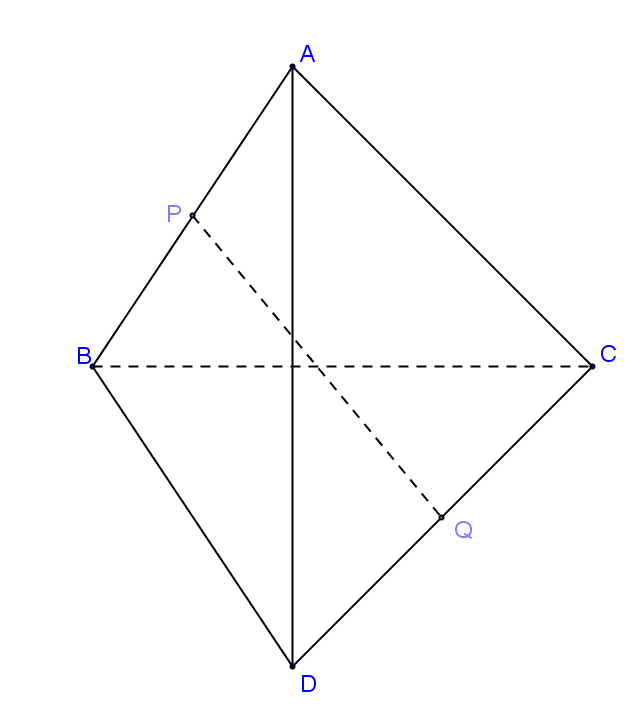
Ta có: \(\overrightarrow {PQ} = \overrightarrow {PA} + \overrightarrow {AC} + \overrightarrow {CQ}\)  

Và: \(\overrightarrow {PQ} = \overrightarrow {PB} + \overrightarrow {BD} + \overrightarrow {DQ}\)  

Do đó: \(2\overrightarrow {PQ} = \overrightarrow {AC} + \overrightarrow {BD}\)  

Vậy: \(2.\overrightarrow {PQ} .\overrightarrow {AB} = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right).\overrightarrow {AB}\)

\(= \overrightarrow {AC} .\overrightarrow {AB} + \overrightarrow {BD} .\overrightarrow {AB} = 0\)

Hay \(\overrightarrow {PQ} .\overrightarrow {AB} = 0\) Tức là: \(PQ \bot AB.\)

Ví dụ 4:

Cho tứ diện ABCD đem AB=AC=AD=a, \(\widehat {BAC} = \widehat {BAD} = {60^0}.\).

a) Chứng minh rằng AB vuông góc CD.

b) Nếu I, J thứu tự là trung điểm của AB và CD thì \(AB \bot IJ.\)  

Hướng dẫn giải:

a) Ta có:

\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {AC}  = \overrightarrow {AB} \left( {\overrightarrow {AD}  - \overrightarrow {AC} } \right)\\
 = \overrightarrow {AB} .\overrightarrow {AD}  - \overrightarrow {AB} .\overrightarrow {AC} 
\end{array}\\
\begin{array}{l}
 = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos BAD\\
\,\,\,\, - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos BAC
\end{array}
\end{array}\)

Mặt không giống tao có: 

\(AB = AC = AD,\widehat {BAC} = \widehat {BAD}\)

Do đó:

\(\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {AC}  = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos BAD\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos BAC = 0
\end{array}\)

Vậy AB vuông góc với CD.

b) Do I, J là trung điểm của AB và CD nên tao có: \(\overrightarrow {IJ} = \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right)\)

Do đó: 

\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {IJ}  = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AD}  + \overrightarrow {AB} \overrightarrow {BC} } \right)\\
 = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AD}  + \overrightarrow {AB} \overrightarrow {BA}  + \overrightarrow {AB} .\overrightarrow {AC} } \right)
\end{array}\\
\begin{array}{l}
 = \frac{1}{2}(\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|\cos {60^0} - {\overrightarrow {AB} ^2}\\
\,\,\,\,\,\,\,\,\,\,\,\, + \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|\cos {60^0})
\end{array}\\
{ = \frac{1}{2}\left( {\frac{1}{2}{a^2} - {a^2} + \frac{1}{2}{a^2}} \right) = 0}
\end{array}\)

Vậy AB và IJ vuông góc nhau.

Xem thêm: Sinh năm 1981 mệnh gì, 1981 tuổi gì? Màu sắc, con số phù hợp

1. Góc thân ái hai vectơ

Cho \(\vec u\) và \(\vec v\) là nhị vectơ vô không khí. Từ một điểm A bất kì vẽ \(\overrightarrow {AB} = \overrightarrow u ,\overrightarrow {AC} = \overrightarrow v\). Khi bại tao gọi góc \(\widehat {BAC}(0 \le \widehat {BAC} \le {180^0})\) là góc thân ái nhị vecto vectơ \(\vec u\) và \(\vec v\), kí hiệu là \(\left ( \vec u ;\vec v \right )\). Ta có: \(\left ( \vec u ;\vec v \right )=\widehat {BAC}\).

2. Tích vô vị trí hướng của nhị vectơ

a) Định nghĩa tích vô vị trí hướng của nhị vectơ

Tích vô vị trí hướng của nhị vectơ \(\vec u\) và \(\vec v\) đều không giống vectơ-không là một số trong những được kí hiệu là \(\vec u .\vec v\) xác dịnh bởi:

\(\vec u.\vec v = \left| {\vec u} \right|.\left| {\vec v} \right|.\cos (\overrightarrow u .\vec v)\)

Nếu \(\vec u= \vec0\) hoặc \(\vec v= \vec0\) thì tao quy ước 

\(\vec u.\vec v=0.\)

b) Tính chất tích vô vị trí hướng của nhị vectơ

Với tía vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c\) trong không khí và với từng số k tao có:

• \(\overrightarrow a .\overrightarrow b = \overrightarrow b .\overrightarrow a\) (tính hóa học phú hoán).
• \(\overrightarrow a (\overrightarrow b + \overrightarrow c ) = \overrightarrow a .\overrightarrow b + \overrightarrow a .\overrightarrow c\) (tính hóa học phân phối).
• \((k.\overrightarrow a ).\overrightarrow b = k.(\overrightarrow a .\overrightarrow b ) = \overrightarrow a .k\overrightarrow b .\)
• \({\overrightarrow a ^2} \ge 0,{\overrightarrow a ^2} = 0 \Leftrightarrow \overrightarrow a = \overrightarrow 0.\)

c) Ứng dụng của tích vô hướng

Xác lăm le góc thân ái nhị vectơ \(\vec u\) và \(\vec v\) bằng \(\cos (\overrightarrow u .\vec v)\) theo đòi công thức: 

\(\cos (\overrightarrow u .\vec v) = \frac{{\vec u.\vec v}}{{\left| {\vec u} \right|\left| {\vec v} \right|}}\)   

3. Vectơ chỉ phương của lối thẳng

Vectơ \(\overrightarrow a \ne \overrightarrow 0\) được gọi là vectơ chỉ phương của đường thẳng liền mạch d nếu như giá chỉ của vectơ \(\overrightarrow a\) song tuy vậy hoặc trùng với đường thẳng liền mạch d.

Nếu \(\overrightarrow a\) là vectơ chỉ phương của đường thẳng liền mạch d thì vectơ \(k\overrightarrow a\) với \(k \ne 0\) cũng là 1 vectơ chỉ phương của d.

Một đường thẳng liền mạch d vô không khí trọn vẹn xác lập được nếu như biết một điểm A nằm trong d và một vectơ chỉ phương \(\overrightarrow a\) của d.

4. Góc thân ái hai tuyến đường thẳng

Góc thân ái hai tuyến đường trực tiếp a và b vô không khí là góc thân ái hai tuyến đường trực tiếp a’ và b’ nằm trong trải qua một điểm bất kì thứu tự tuy vậy song với a và b.

5. Hai đường thẳng liền mạch vuông góc

a) Định nghĩa

Hai đường thẳng liền mạch a và b gọi là vuông góc cùng nhau nếu như góc thân ái bọn chúng vì như thế 90⁰.

Ta kí hiệu là: \(b \bot a\) hoặc \(a \bot b.\)

b) Tính chất

• Nếu \(\vec u\) và \(\vec v\) lần lượt là những vectơ chỉ phương của hai tuyến đường trực tiếp a và b thì: \(a \bot b \Leftrightarrow \overrightarrow u .\overrightarrow v = 0.\)
• Cho hai tuyến đường trực tiếp tuy vậy tuy vậy. Nếu một đường thẳng liền mạch vuông góc với đường thẳng liền mạch này thì cũng vuông góc với đường thẳng liền mạch bại.
• Hai đường thẳng liền mạch vuông góc nhau thì rất có thể hạn chế nhau hoặc chéo cánh nhau.

6. Bài luyện minh họa

Ví dụ 1:

Cho hình lập phương ABCD.EFGH. Hãy xác lập góc trong số những cặp vectơ sau đây:

a) \(\overrightarrow {AB} ,\overrightarrow {EG} .\)

c) \(\overrightarrow {AB} ,\overrightarrow {DH}\).

Hướng dẫn giải:

a) Vì EG // AC nên góc giữa 

\(\overrightarrow {AB} ,\overrightarrow {EG}\) cũng vì như thế góc giữa 

\(\overrightarrow {AB}\) và \(\overrightarrow {AC}\)

Vậy \(\left( {\overrightarrow {AB} ;\overrightarrow {EG} } \right) = \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = {45^0}.\)

b)  Vì AB // DG nên góc giữa \(\overrightarrow {AB} ,\overrightarrow {DH}\) cũng vì như thế góc giữa \(\overrightarrow {DC}\) và \(\overrightarrow {DH}\)

Vậy \(\left( {\overrightarrow {AB} ;\overrightarrow {DH} } \right) = \left( {\overrightarrow {AB} ;\overrightarrow {DH} } \right) = {45^0}.\)

Ví dụ 2:

Cho hình chóp tam giác S.ABC đem SA = SB = SC và đem \(\widehat {{\rm{ASB}}} = \widehat {BSC} = \widehat {CSA}.\)

Chứng minh rằng: \(SA \bot BC, SB\bot AC, SC \bot AB.\)

Hướng dẫn giải:

Xét những tích vô hướng: 

\(\overrightarrow {SA} .\overrightarrow {BC} ,\overrightarrow {SB} .\overrightarrow {AC} ,\overrightarrow {SC} .\overrightarrow {AB} .\)

Ta có: 

\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {SA} .\overrightarrow {BC}  = \overrightarrow {SA} .(\overrightarrow {SC}  - \overrightarrow {SB} )\\
 = \overrightarrow {SA} .\overrightarrow {SC}  - \overrightarrow {SA} .\overrightarrow {SB} 
\end{array}\\
\begin{array}{l}
 = \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {SC} } \right|.\cos \widehat {CSA}\\
\,\,\,\,\,\,\,\,\, - \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {SB} } \right|\cos \widehat {ASB}
\end{array}
\end{array}\)

Theo giá chỉ thuyết: \(\left| {\overrightarrow {SB} } \right| = \left| {\overrightarrow {SC} } \right|\)

Và: \(\cos \widehat {CSA} = \cos \widehat {ASB} \Rightarrow \overrightarrow {SA} .\overrightarrow {BC}  = 0\)

Vậy: \(SA \bot BC.\)

Chứng minh tương tự động tao có: 

\(SB\bot AC, SC \bot AB.\)

Ví dụ 3:

Cho tứ diện ABCD đem AB ⊥ AC và AB ⊥ BD. Gọi P.. và Q thứu tự là trung điểm của AB và CD. Chứng minh rằng AB và PQ là hai tuyến đường trực tiếp vuông góc cùng nhau.

Hướng dẫn giải:

Ta có: \(\overrightarrow {PQ} = \overrightarrow {PA} + \overrightarrow {AC} + \overrightarrow {CQ}\)  

Và: \(\overrightarrow {PQ} = \overrightarrow {PB} + \overrightarrow {BD} + \overrightarrow {DQ}\)  

Do đó: \(2\overrightarrow {PQ} = \overrightarrow {AC} + \overrightarrow {BD}\)  

Vậy: \(2.\overrightarrow {PQ} .\overrightarrow {AB} = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right).\overrightarrow {AB}\)

\(= \overrightarrow {AC} .\overrightarrow {AB} + \overrightarrow {BD} .\overrightarrow {AB} = 0\)

Hay \(\overrightarrow {PQ} .\overrightarrow {AB} = 0\) Tức là: \(PQ \bot AB.\)

Ví dụ 4:

Cho tứ diện ABCD đem AB=AC=AD=a, \(\widehat {BAC} = \widehat {BAD} = {60^0}.\).

a) Chứng minh rằng AB vuông góc CD.

b) Nếu I, J thứu tự là trung điểm của AB và CD thì \(AB \bot IJ.\)  

Hướng dẫn giải:

a) Ta có:

\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {AC}  = \overrightarrow {AB} \left( {\overrightarrow {AD}  - \overrightarrow {AC} } \right)\\
 = \overrightarrow {AB} .\overrightarrow {AD}  - \overrightarrow {AB} .\overrightarrow {AC} 
\end{array}\\
\begin{array}{l}
 = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos BAD\\
\,\,\,\, - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos BAC
\end{array}
\end{array}\)

Mặt không giống tao có: 

\(AB = AC = AD,\widehat {BAC} = \widehat {BAD}\)

Do đó:

\(\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {AC}  = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos BAD\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos BAC = 0
\end{array}\)

Vậy AB vuông góc với CD.

b) Do I, J là trung điểm của AB và CD nên tao có: \(\overrightarrow {IJ} = \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right)\)

Xem thêm: Sinh năm 1981 mệnh gì? Tân Dậu hợp màu gì, tuổi nào, hướng nào?

Do đó: 

\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {IJ}  = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AD}  + \overrightarrow {AB} \overrightarrow {BC} } \right)\\
 = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AD}  + \overrightarrow {AB} \overrightarrow {BA}  + \overrightarrow {AB} .\overrightarrow {AC} } \right)
\end{array}\\
\begin{array}{l}
 = \frac{1}{2}(\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|\cos {60^0} - {\overrightarrow {AB} ^2}\\
\,\,\,\,\,\,\,\,\,\,\,\, + \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|\cos {60^0})
\end{array}\\
{ = \frac{1}{2}\left( {\frac{1}{2}{a^2} - {a^2} + \frac{1}{2}{a^2}} \right) = 0}
\end{array}\)

Vậy AB và IJ vuông góc nhau.