Một kỹ thuật chứng minh tam giác đồng dạng và áp dụng
- 07/03/2023
- 237 lượt xem
- bqttoancasio
Giả sử ta có hai tam giác đồng dạng $ABC$ và $A’B’C’$ , các góc tương ứng bằng nhau như hình vẽ:
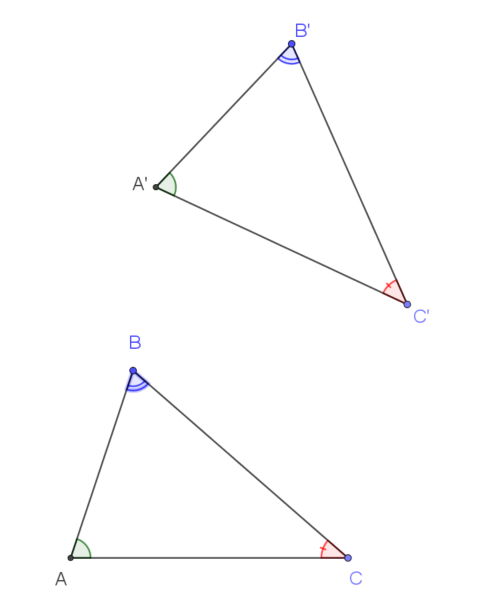
lấy $A’$ làm tâm vị tự điểm $C’$ thành điểm $C’_1$ theo cùng tỉ số $k$:
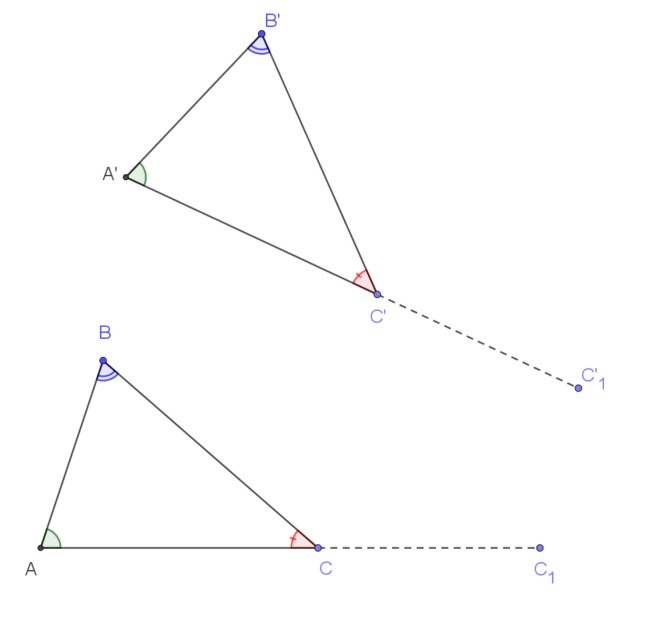
Khi đó hai tam giác $ABC_1$ và $A’B’C’_1$ nối hai đỉnh cũ và đỉnh mới lập thành hai tam giác đồng dạng. Chú ý hai trường hợp đặc biệt: nếu $k=\dfrac12$: “thu về trung điểm “, nếu $k=2$: “phóng ra gấp đôi “
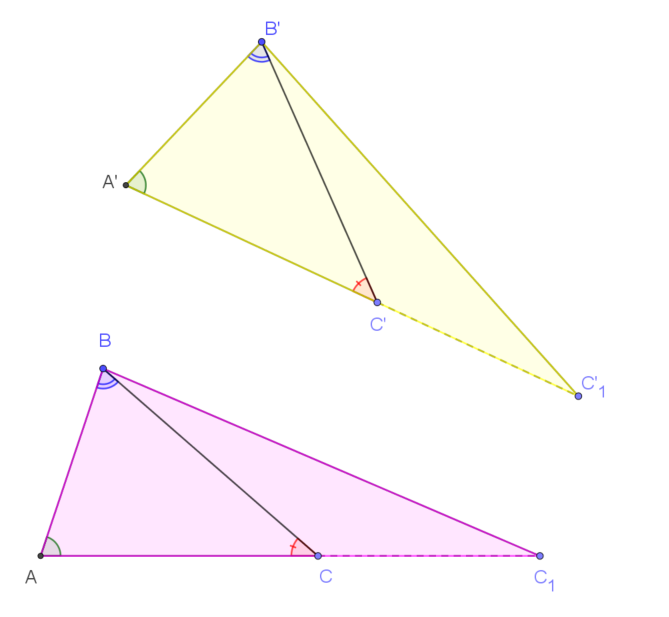
Giả sử tam giác $ABC$ đồng dạng với tam giác $A’B’C’$ và $\widehat{A}=\widehat{A’} ; \dfrac{AC}{AB}=\dfrac{A’C’}{A’B’}$
$ ⇒ \dfrac{k.AC}{AB}=\dfrac{k.A’C’}{A’B’} ⇒ \dfrac{AC_1}{AB}=\dfrac{A’C’_1}{A’B’}$.
Hai tam giác $ABC_1$ và $A’B’C’_1$ có: $\widehat{A}=\widehat{A’} ; \dfrac{AC_1}{AB}=\dfrac{A’C’_1}{A’B’}$ nên là hai tam giác đồng dạng.
Cho tam giác $ABC$ ngoại tiếp đường tròn $(O)$, các cạnh $BC, CA, AB$ tiếp xúc với đường tròn này lần lượt tại $M, N, P$. Hạ $MK$ vuông góc với $NP$. Chứng minh $KM$ là đường phân giác cúa góc $\widehat{BKC}$.
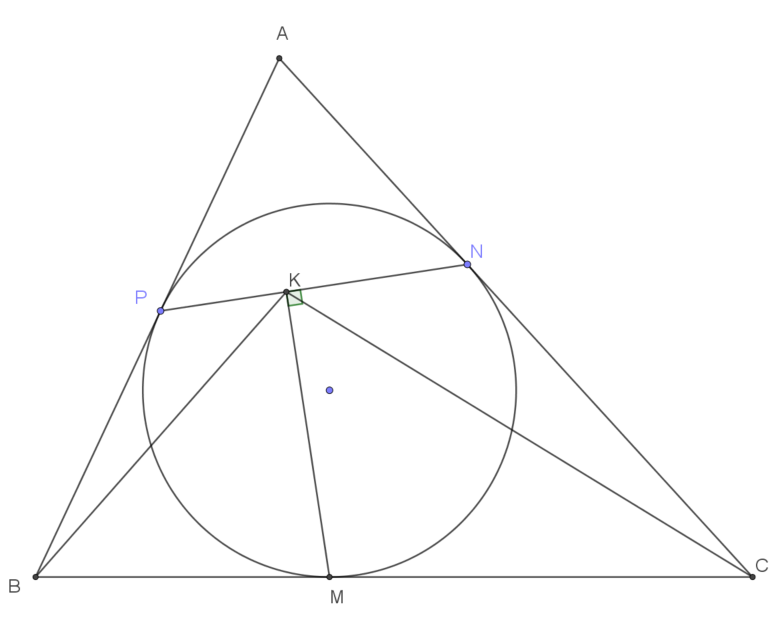
- 1. Ta chỉ cần chứng minh $\widehat{BKP}=\widehat{CKN}$. Vì ta thấy $\widehat{KPB}=\widehat{KNC}$ nên ta chứng minh hai tam giác $BKP$ và $CKN$ đồng dạng.
- 2. Để chứng minh $\triangle BKP\backsim \triangle CKN$ ta lấy $K$ làm tâm vị tự điểm $P$ thành điểm $E$ ưu tiên tạo thành tam giác vuông. Sau đó lấy $K$ làm tâm vị tự điểm $N$ thành điểm $F$ để tạo thành tam giác vuông.
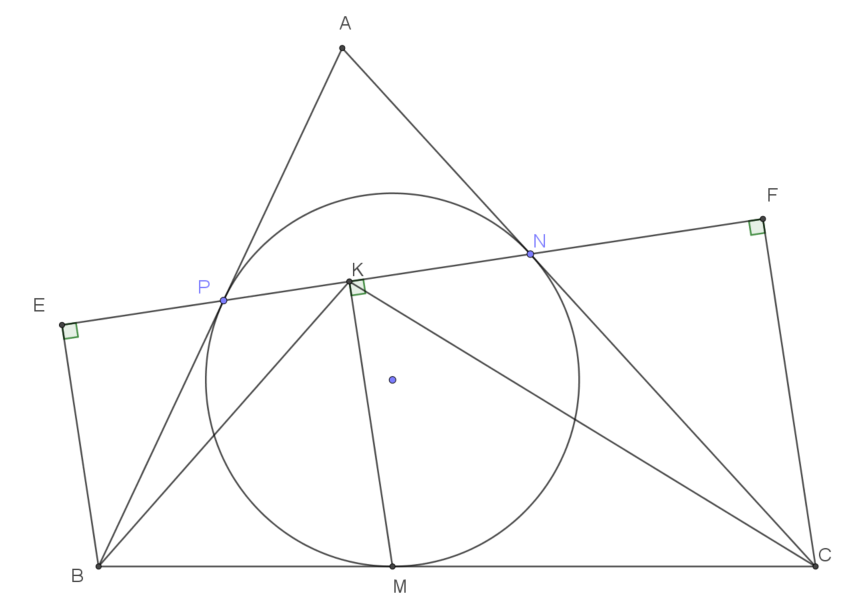
- 3. Để chứng minh $\triangle BKE \backsim \triangle CKF$ ta chỉ cần chứng minh $\triangle BPE \backsim \triangle CNF$. Hai tam giác vuông vày đồng dạng vì có góc $\widehat{BPE}=\widehat{CNF}$ (đối đỉnh với hai góc bằng nhau).
Chứng minh
Hạ $BE$ và $CF$ vuông góc với đường thẳng $NPP$. Hai tam giác $BPE$ và $CNF$ có:
$$\left\lbrace\begin{array}{l}\widehat{BEP}=\widehat{CFN}=90^\circ\\
\widehat{BPE}=\widehat{CNF}\quad \text{(vì lần lượt đối đỉnh với hai góc bằng nhau}\ \widehat{APN}\ \text{và}\ \widehat{ANP}) \end{array} \right. $$
Suy ra hai tam giác này đồng dạng. Do đó: $\dfrac{PE}{PB}=\dfrac{NF}{NC}\quad (1)$
Áp dụng định lý Thales vào hình thang ta có: $$\dfrac{KE}{KF}=\dfrac{MB}{MC} =\dfrac{PB}{NC} \Leftrightarrow \dfrac{KE}{PB}=\dfrac{KF}{NC}\quad (2)$$
Lấy (2) trừ (1) ta có: $\dfrac{PK}{PB}=\dfrac{NK}{NC}$, ngoài ra $\widehat{BPK}=\widehat{CNK} $ vì lần lượt bù với hai góc bằng nhau $\widehat{BPE}$ và $\widehat{CNF}$ nên $\triangle BPK \backsim \triangle CNK ⇒ \widehat{PKB}=\widehat{NKC} ⇒ \widehat{BKM}=\widehat{CKM}$ (đpcm).
Bài Viết Tương Tự
SỬ DỤNG MÁY TÍNH FX-880BTG KIỂM TRA SỐ NGUYÊN TỐ
Một số nguyên là số nguyên tố khi và chỉ khi nó không chia hết …











